基于晶振的无稳态触发器设计

目录

　　在计算机系统和通信系统中，控制和协调整个系统的矩形脉冲信号源主要依靠无稳态触发器提供。构成无稳态触发器的电路很多，其中由集成门电路构成的无稳态触发器，其电路结构简单，应用广泛。基于集成门电路的无稳态触发器种类较多，大致可分为积分型无稳态触发器和非对称式及对称式微分型无稳态触发器。但这些无稳态触发器都有一个共同的缺点：振荡频率的稳定度和准确性不太高，其主要原因一是转换电平由阈值电压决定，而阈值电压本身极容易受温度、电源电压变化的影响;二是电路的翻转靠电容充放电电平逐渐趋于门限电压，而充放电是按指数规律，变化较缓慢，因此转换电平微小变化或干扰都会严重影响振荡周期。根据以上情况，本文设计了一种振荡频率稳定、性能可靠的无稳态触发器。

　　1.石英晶体工作原理

　　石英晶体谐振器是利用石英晶体(二氧化硅的结晶体)的压电效应制成的一种谐振器件，有极好的选频特性。所谓压电效应即是：在石英晶体的两个电极上加一电场，晶片就会产生机械变形;反之，在晶片的两侧施加机械压力，则在晶片相应的方向上产生电场。如果在晶片的两极上加交变电压，晶片就会产生机械振动，同时晶片的机械振动又会产生交变电场。在一般情况下，晶片机械振动的振幅和交变电场的振幅非常小，但当外加交变电压信号的频率为某--特定值时，振幅会明显加大，比其他频率下的振幅大得多，这种现象称为压电谐振，它与LC回路的谐振现象十分相似。所以，其内部电路可用一组串联的电阻R、电容C、电感L与电容C0并联来等效，如图1(a)所示，图1(b)为其符号表示。当晶体不振动时，可把它看成一个平板电容C0称为静电电容。当晶体振荡时，机械振动的惯性可用电感L来等效，晶片的弹性可用电容C来等效，晶片振动时因摩擦而造成的损耗可用电阻R来等效。由于晶片的等效电感L很大，而电容C很小，电阻R也小，因此回路的品质因数Q很大，可达104-106。

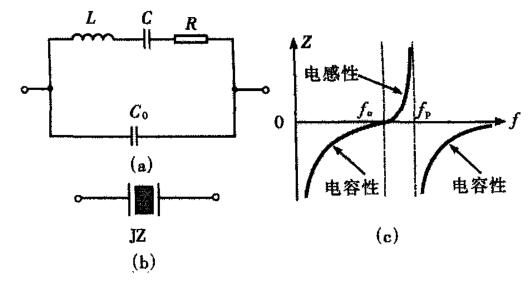
　　图1 等效电路、符号和特性

　　石英晶体的电抗特性如图1(c)所示，其中f0是电容C和电感L的的串联谐振频率，fp是石英晶体并联谐振频率。因为在石英晶体呈电感性所对应的f0-fp内，英晶体具有极陡峭的电抗特性曲线，对频率变化具有极灵敏的补偿能力。所以石英晶体工作频率常定在f0或f0—fp内：工作频率常为f0，晶体阻抗为零;工作频率常在f0一fp内，晶体呈电感性，此时还可通过串接一个电容来微调输出频率。一般来说，fp一f0之差很小，例如对f0为几MHz的石英晶体，fp一f0不过几十至几百赫[兹]。即每一块石英晶体的谐振频率基本上是固定的。所以，晶片本身的谐振频率基本上只与晶片的切割方式。几何形状、尺寸有关，而且可以做得很精确，因此利用石英晶体组成的振荡电路可获得很高的频率稳定度，完全可以满足大多数数字系统对频率稳定度的要求。

　　2.无稳态触发器设计

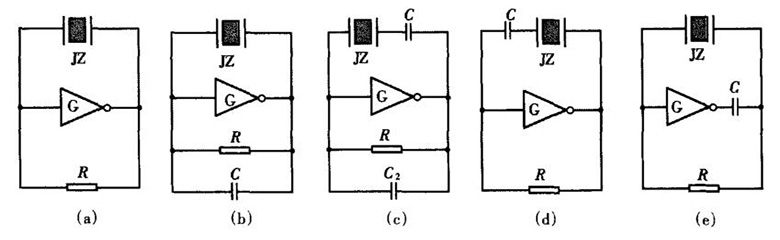
　　图2 简单无稳态触发器组成

　　利用石英晶体构成的振荡器不仅频率稳定性好而且选择性也很好，所以目前普遍采用在由集成门电路组成的无稳态触发器中接入石英晶体，组成石英晶体无稳态触发器，来实现高精度的频率要求。其电路通常有串联型石英晶体无稳态触发器电路和并联型石英晶体无稳态触发器电路。在串联型电路中，当外加电压的频率fs等于石英晶体的固有频率f0时，石英晶体的等效阻抗为零，电路的振荡频率取决于石英晶体的固有频率，石英晶体相当于作为放大电路的反馈网络，并起选频作用。以图2(b)、图2(c)所示的无稳态触发器为例，在其电容C的输入端串接一个石英晶体便构成了微分型石英晶体无稳态触发器;在并联型电路中，石英晶体的阻抗呈电感性，则将它与外接电容构成电容三点式无稳态触发器电路。

　　由于石英晶体在工作中它的二极呈一交变压电，这使之具有反相器的输人信号与输出信号之间的反相关系，因此由之产生一种把石英晶体与反相器并接的设计方案。此时只要给反相器并联一个偏置电阻，使反相器工作在传输特性的线性放大区，就能组成了一个结构最简单的石英晶体无稳态触发器，如图2(a)所示。该电路的输出频率与石英晶体的固有频率完全相同，不可微调，为此可用与石英晶体并接、串接，或既并接又串接小电容的方法，通过改变电容的值来实现频率的微调，如图2(b)、图2(e)所示。在这些电路图中，可以发现，图2(d)、图2(e)与图2(b)所示的“非对称式微分型无稳态触发器"在结构上相关。二者的区别是图2(d)用石英晶体替代图2(b)中的反相器G0，而图2(e)则是用石英晶体取代图2(b)中的反相器G1。

　　由此我们得到启发：由于石英晶体在工作时，其二端的极性相反，具有选频兼移相180°的作用，因此可用来替代图2(b)所示的“非对称式微分型无稳态触发器”中的反相器。这种替代法也同样适用于对称式微分型无稳态触发器。经计算机模拟和实际电路验证，如把图2(c)所示的对称式微分型无稳态触发器中的任一反相器替换成石英晶体，即可实现石英晶体无稳态触发器。但这一替代法对于图2(a)所示的积分型无稳态触发器就不适用，因为石英晶体替代任何一个反相器后都不可能使它两端的信号相位相差180°。

　　另一方面，由石英晶体的电抗频率特性可知，石英晶体的振荡频率取决于石英晶体的固有频率f0，与外接电阻、电容的参数无关，因此在选频电路中，常将与晶体串联的电容省去。如在图2(a)中，虽不能用石英晶体取代任一反相器，但可把石英晶体与电容C串联来选取稳定可靠的频率，而且还可通过电容C来适当微调输出频率。考虑到石英晶体的振荡足够稳定，可以将微调电容C省去，由此便可得到图3所示的“积分型石英晶体环形多谐振荡器”，苏即积分型石英晶体无稳态触发器。上述过程从形式上看是用石英晶体直接取代电容，实质上是利用石英晶体的选频作用和电抗频率特性。同理，也可在图2(b)、(c)所示的对称式(或不对称式)微分型无稳态触发器中，将其中的一个电容用石英晶体取代后实现另一种石英晶体微分型无稳态触发器。

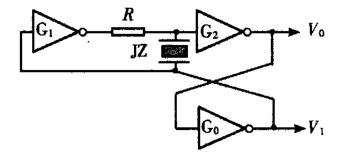
　　图3 积分型石英晶体环形多谐振荡器

　　结语

　　以上就是基于晶振的无稳态触发器设计介绍了。本文将通过对石英晶体振荡器和基于集成门电路构成的无稳态触发器工作原理的深入研究，探索一系列电路结构更简单的石英晶体无稳态触发器，并运用Elec-tronics Workbench EDA5.Q计算机软件仿真技术和实际电路测试技术验证其结果的正确性。