AD603点击型号即可查看芯片规格书
目录
超声探伤仪已经在机械零件内部缺陷的检测领域发挥巨大作用。其原理是电压激励超声换能器向零件中发射超声波,被缺陷反射的超声波回到换能器,转化成电压,该电压经信号放大电路放大后显示出来,从而传递出零件内部缺陷的信息。由于缺陷反射波电压从几毫伏至几百毫伏不等,故信号放大电路必须有按需调整放大倍数的能力。根据《A型脉冲反射式超声探伤仪通用技术条件(JB/T10061—1999)》,超声探伤仪的增益调整范围至少达到60dB。因此本文设计一种以集成运算放大器AD603为核心,辅以高速运算放大器AD8041的超声探伤仪信号放大电路。
信号放大电路整体结构如图1所示,由两片AD603级联,每片之前采用AD8041构成的反相比例放大器进行阻抗匹配。
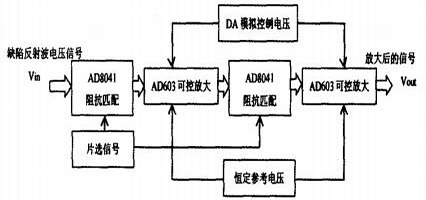
图1 信号放大电路整体结构
AD603采用并联控制方式,即两片的控制电压始终保持一致,故总体增益是单片AD603增益的两倍。图中,“恒定参考电压”由电压基准芯片产生,“DA模拟控制电压”是由数模转换芯片产生的可控直流电压。AD8041有一个芯片使能引脚,使用一个片选信号进行控制,可以决定芯片是否工作。这一功能在多通道信号放大电路轮流工作时将发挥作用。
AD603是一种集成运算放大器,图2为其内部结构简图。3号引脚VINP为信号输入端,7号引脚VOUT为信号输出端。通过改变1号引脚GPOS和2号引脚GNEG之间的电压差,可以控制接入电路的梯形网络范围,从而控制芯片增益。具体设计中,“恒定参考电压”供给2号引脚GNEG,“DA模拟控制电压”供给1号引脚GPOS。设计采用5、7号引脚直接短接的方式,获得单片AD603增益调整范围一1ldB至+31dB,共计42dB。因此,放大电路整体的增益调整范围为84dB。
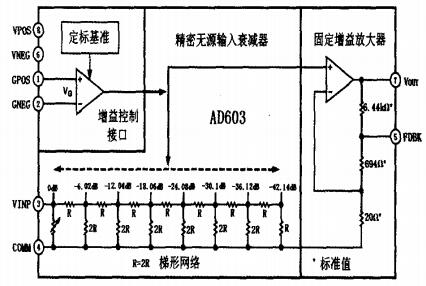
图2 AD603内部结构简图
增益计算公式是:
Gain(dB)=40VG(dB/V)+10(dB)
其中,VG为引脚GPOS和GNEG之间的电压差(单位V)。由于GNEG等于“恒定参考电压”,保持不变,故调整“DA模拟控制电压”,就可以改变VG,从而控制增益。
根据AD603数据手册,必须在负载电阻大于500Ω时,AD603输出电压才能达到峰值±3V;其输入电阻典型值为100Ω。因此,如果两片AD603直接级联,会由于后级的输入阻抗过小而造成前级的增益低于预期。另外,如果反射波电压信号直接输入AD603,也会由于输入阻抗过小而造成信号失真。
为解决这一问题,设计采用高速运算放大器AD8041搭建反相比例放大电路(如图3所示)起到阻抗匹配的作用。
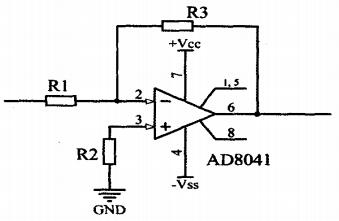
图3 AD8041反比例放大电路
反相比例放大电路输入电阻公式为:
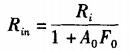
其中,Ri为运放的开环输入电阻,根据AD8041数据手册,Ri=160kΩ;A0为其开环放大系数,在超声波频率(2.5MHz)时A0=35dB,即56.23倍(根据AD8041开环频响曲线确定,如图4所示);F0为负反馈系数,数值上等于R1与R3,电阻值之比,实验中取0.05。带入计算得,Rin=41.98kΩ>500Ω。因此,AD8041可以提供足够的输入电阻。
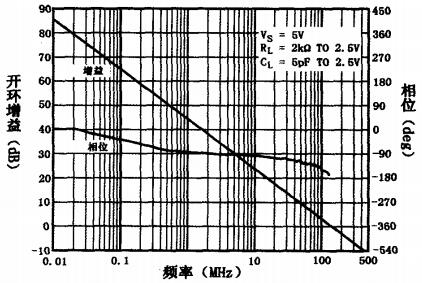
图4 AD8041开环频响曲线
另外,根据AD8041数据手册,负载电阻50Ω时,输出电压可以达到4.5V,接近饱和。因此,AD8041可以驱动AD603。
实验发现,当AD603增益较大时,电路极易产生高频自激现象,现将其生成机理建模分析如下。首先介绍负反馈自激振荡的经典理论。一般的负反馈电路可以抽象成如图5所示的模型。发生自激振荡的条件是:
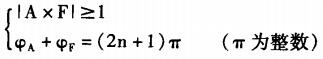
其中,A为开环传递函数,F为负反馈传递函数。就图1信号放大电路而言,每一级运放负反馈都是纯电阻网络反馈,而且运放的开环相位延迟恒小于180°,故单级运放不满足自激条件。然而,印刷电路板不可避免要引入寄生电容,在超声波频率及其高频谐波的量级上(2.5MHz至25MHz),它会引起各级之间的反馈。这里只考虑最后一级输出信号到第一级AD8041的输入的反馈,建立图6所示的模型。
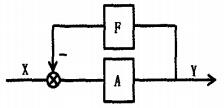
图5 一般负反馈电路
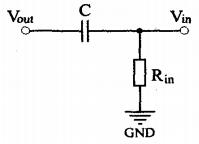
图6 寄生负反馈模型
其中,C是上述两端之间的寄生电容,假设其值仅有0.1pF;Rin为第一级AD8041的输入电阻,前文已计算得,Rin=41.98kQ。它们实际上构成了一个无源高通滤波器。由于负反馈电路模型(图5)中F指的是负反馈的传递函数,故图6的模型向整个电路中引入的负反馈传递函数为:
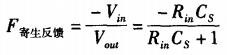
其频率响应曲线如图7所示。
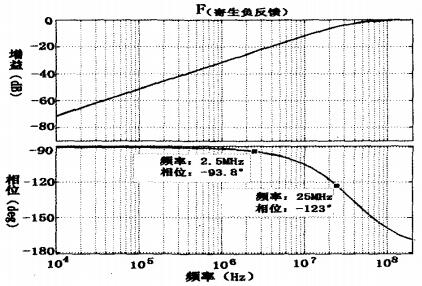
图7 寄生负反馈频响曲线
可见,2.5MHz至25MHz频率时的相位响应为.﹣93.8°至﹣123°,对比自激振荡的条件可知,只要四个级联的运放能在这一频段上提供﹣86.2°至﹣57°的相位响应和足够大的放大系数就可以发生自激振荡。根据AD603数据手册,它在这一频段闭环传递函数的相位延迟很小,故这里只考虑AD8041闭环传递函数引起的相位延迟。每个AD8041闭环传递函数只要提供﹣43.1°至﹣28.5°的相位响应就满足了自激振荡的相位要求。
根据AD8041的开环频率响应(如图4所示),其开环传递函数包含两个惯性环节和一个比例环节,极点对应的频率分别为:f1=0.1MHz和f2=90MHz,比例系数K=2000。故开环传递函数表达式:
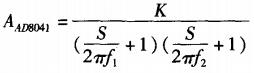
则图3所示的AD8041闭环传递函数为:
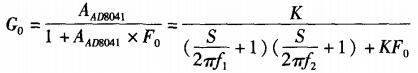
其频率响应曲线如图8所示。可见,2.5MHz至25MHz频率时的相位响应为﹣14.1°至﹣82.8°,因此在这一频段必有一点的相位响应契合﹣43.1°至﹣28.5°的相位要求,满足自激振荡条件。
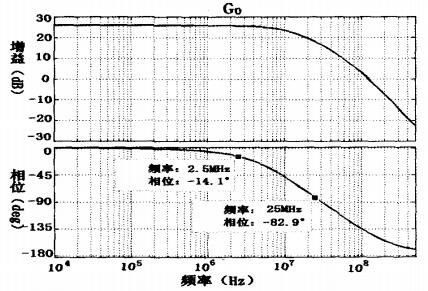
图8 AD8041闭环频响曲线
通过在反相比例放大电路(如图3所示)的电阻R,上并联小值电容C。(经实验确定取值20pF)构成超前补偿,可以破坏自激振荡的相位条件,从而消除这一现象。
超前补偿后的负反馈传递函数为:
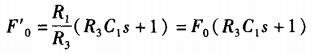
故新的闭环传递函数为:
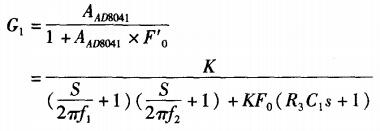
其频率响应曲线如图9所示。
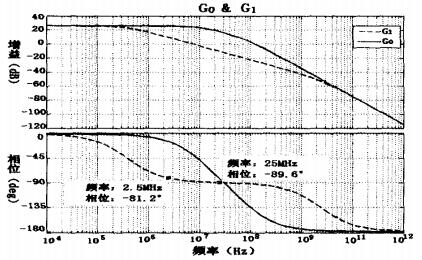
图9 引入超前补偿前后频晌曲线比较
可见,引入超前补偿后,闭环传递函数从典型的振荡环节变为两个惯性环节,幅频响应略有下降,但相频响应产生了巨大变化。在需要关注的2.5MHz到25MHz频上,相频响应基本稳定在﹣90°,那么两级AD8041超前补偿的相频响应为﹣180°,不可能提供﹣43.1°至﹣28.5°的相位条件。由此可见,超前补偿可以从根本上消除自激振荡。
本文总结了基于AD603的超声探伤仪信号放大电路设计方案,该设计采用两片增益可控的集成运算放大器AD603级联的方式,实现了增益调整范围84dB的信号放大电路。通过建模分析了实验过程中四级运算放大器级联产生自激振荡的机理,采取超前补偿可以破坏自激振荡的相位条件,从而从根本上解决了该问题。