基于模拟电感的混沌同步电路设计

目录

　　如今，电子元件逐渐小型化，而在集成电路中要减小电阻和电容器的尺寸是比较简单的，至于无源电感器，体积庞大，不利于集成。这是因为半导体内得不到电磁效应，而半导体又是集成电路的主要材料，因此组成铁芯的磁物质和组成电感绕组的导线必须沉积在半导体的表面上，这种结构只能得到很低的电感量;再者电感器的尺寸与品质因数也有很大的关系，尺寸越小其品质因数也越小，因而微小的电感通常是不能应用的。因此，为了在电路中消除电感，可以用有源器件来模拟电感。所谓模拟电感器，就是将电路中每个电感用一个综合电路来代替，这个理论使电感元件在电路中实现微型化、片型化和集成化。本文将模拟电感应用于混沌电路，并进行了仿真。

　　1.混沌与混沌同步原理

　　所谓混沌是指确定性系统产生的类似随机的输出。所谓确定性电路是指电路的参数和输入都为确定值，没有随机因素。所谓不确定、类似随机的输出是指电路的输出既不是周期的，又不是拟周期的;既不趋于无穷、又不趋于静止，而是在一定区域内呈现永不重复的输出。总体上说，混沌同步属于混沌控制的范畴，迄今已发现了几种类型的混沌同步，其中一种类型就是Pceora和Carroll提出的同步方案。该方案电路中存在驱动与被驱动的关系，其中驱动电路可分为稳定部分和不稳定部分，将其中的稳定部分复制一个响应，然后把响应系统与驱动系统用驱动信号耦合起来，由此可达到相应系统与驱动系统同步。

　　混沌现象广泛的存在于非线性电路中，比较典型并已得到深入研究的电路是蔡氏电路。蔡氏电路如图1(a)所示。电路中的非线性由一个分段线性的负电阻引入，非线性电阻的伏安特性如图1(b)所示。

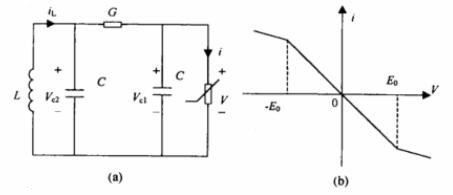
　　图1 蔡氏电路及分段线性电阻

　　当电路的参数满足一定的条件时，将会产生成为双涡卷的自激振荡吸引子。图2就是一个蔡氏混沌同步电路。

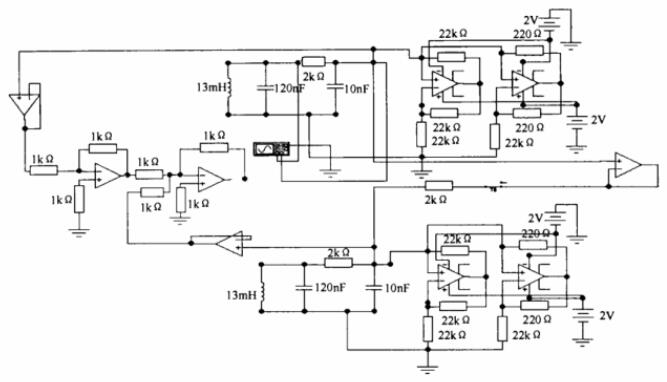
　　图2 蔡氏混沌同步电路

　　2.模拟电感器

　　常用三种的模拟电感电路：里奥登电感电路、无损模拟电感电路及低损耗模拟电感电路。

　　2.1里奥登电感电路

　　该电路(图3)是由2个集成运放、4个电阻及1个电容构成。由于运放被视作理想集成运放，因此开环差模电压放大倍数Aod≦∞，流入两输入端的电流I+≦I_≦0，U+≦U_。

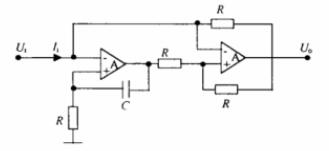
　　图3 里奥登电感电路

　　第一个运放实现的是同相比例运算电路，因此可以得到：

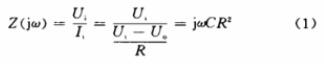
　　因此，里奥登电路可以等效为一个L=R2C的模拟电感。

　　2.2新型无损模拟电感电路

　　该电路(图4)由1个运放、4个电阻及2个电容组成。Ui为输入信号，Uo为输出信号。由理想运放的特点，可以得出：

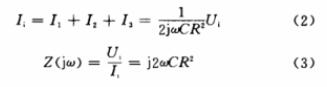
　　因此，该电路可以等效为一个L=2R2C的模拟电感。

　　图4 无损模拟电感电路

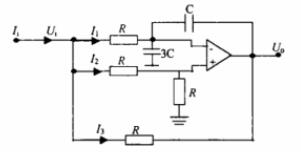
　　2.3低损耗模拟电感电路

　　该电路(图5)是由1个运放、4个电阻及1个电容组成。Ui为输入信号，Uo为输出信号。

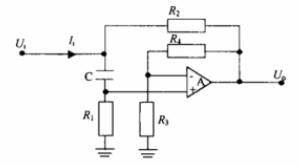
　　图5 低损耗模拟电感电路

　　根据理想运放的特点，可以列出：

　　令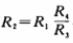，则可以得到：

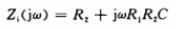
　　由此可以得出，此电路可以等效为一个电阻与一个L=R1R2C的串联组合。

　　3.仿真研究

　　将图2中的电感分别用上述3种模拟电感分别替换进行仿真。观察用18mH模拟电感代替实际电感时3个电路的时域波形、混沌吸引子及输出电压频谱。

　　3.1里奥登电路的应用

　　将前面介绍的里奥登电路中的参数取R=1kΩ，电容C=18nF，则里奥登电路可相当于L=R2C=(103)2×18×10-9=18mH的电感。

　　将其应用于混沌同步电路中得到的时域波形、混沌吸引子及电压频谱如图6所示。

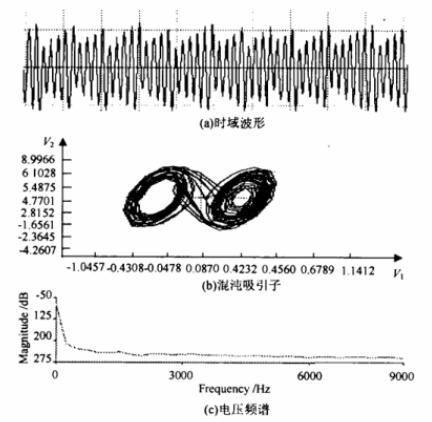
　　图6 里奥登电路的应用

　　3.2新型无损模拟电感电路的应用

　　将前面介绍的无损模拟电感电路中的参数取R=1kΩ，C=9nF，则此新型模拟电感电路可等效为一个L=2R2C=2×(103)2×9×10-9=18mH的电感。

　　将其应用于混沌同步电路中得到的时域波形、混沌吸引子及电压频谱如图7所示。

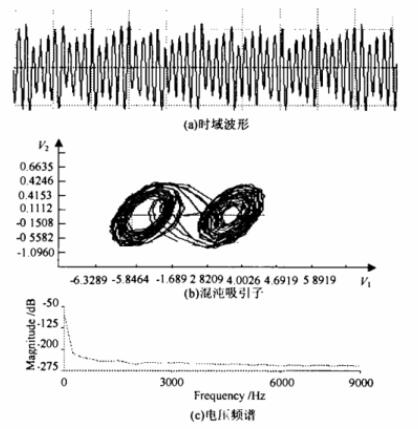
　　图7 新型无损模拟电感电路的应用

　　3.3低损耗模拟电感电路的应用

　　将前面介绍的低损耗模拟电感电路中的参数取R4=R2=0.05kΩ，R1=R3=4kΩ,C=90nF则此低损耗模拟电感电路可等效为一个L=R1R2C=4×103×0.05×103×90×10-9=18mH的电感。

　　将其应用于混沌同步电路中得到的时域波形、混沌吸引子及电压频谱如图8所示。

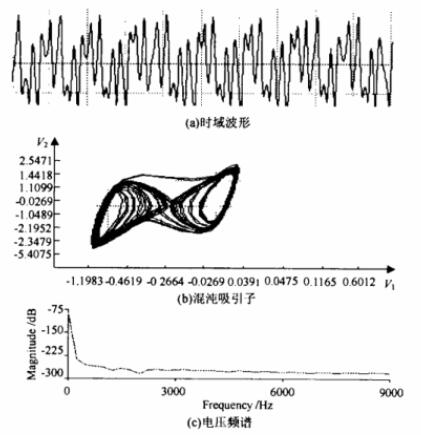
　　图8 低损耗模拟电感电路的应用

　　结语

　　以上就是基于模拟电感的混沌同步电路设计与研究介绍了。通过仿真研究发现，模拟电感可以代替实际中的电感，而不影响混沌电路的混沌特性，基于模拟电感的混沌电路不但具有白噪声的频谱特征，而且自相关函数具有接近于δ函数的性态，这为开发研究集成功能的混沌振荡器提供了条件。并且具有体积小、便于集成的特点，具有非常广泛的应用前景。