AD9445点击型号即可查看芯片规格书
为实现高信噪比(SNR),ADC的孔径抖动必须很低。目前可提供孔 径抖动低至60 fs rms的ADC(AD9445 14位125MSPS和AD9446 16位100MSPS)。为了避免降低ADC的性能,必须采用抖动极低的采样时钟,因为总抖动等于转换器内部孔径抖动与外部采样时钟抖动的方和根。然而,用于产生采样时钟的振荡器常常用相位噪声而非时间抖动来描述特性。本文的目的就是提出一种简单的方法来将振荡器相位噪声转换为时间抖动。
相位噪声定义
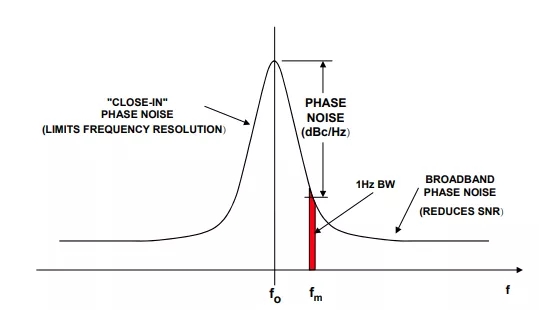
首先明确几个定义。图1所示为一个非理想振荡器(即时域中存在抖动,对应于频域中的相位噪声)的典型输出频谱。频谱显示,1Hz带宽内的噪声功率与频率成函数关系。相位噪声定义为额定频率偏移fm下的1Hz带宽内的噪声与频率fO下的振荡器信号幅度之比
图1:受相位噪声影响的振荡器功率频谱
采样过程基本上是采样时钟与模拟输入信号的乘法。这是时域中的乘法,相当于频域中的卷积。因此,采样时钟振荡器的频谱与输入进行卷积,并显示在纯正弦波输入信号的FFT输出上(见图2)。
图2:采样时钟相位噪声对理想数字化正弦波的影响
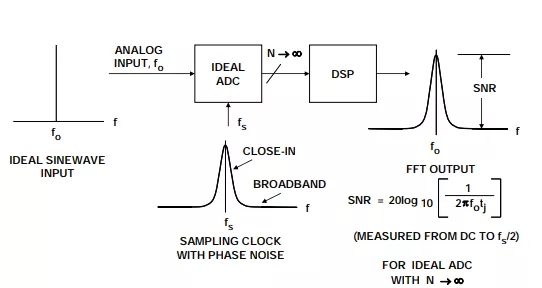
“近载波”相位噪声会“污损”多个频率仓中的基波信号,从而降低整体频谱分辨率。“宽带”相位噪声则会导致整体SNR下降,如公式1所示:
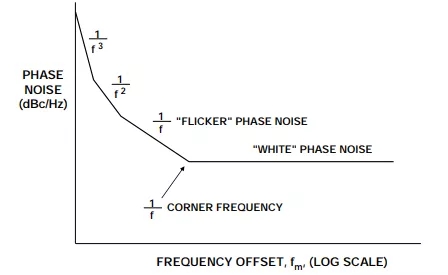
通常用单边带相位噪声来描述振荡器的特性,如图3的相位噪声(dBc/Hz)与频率偏移fm的关系曲线所示,其中频率轴采用对数刻度。注意,实际的曲线由多个区域拟合而成,各区域的斜率为1/fx ,x=0对应于“白色”相位噪声区域(斜率=0dB/10倍),x=1对应于“闪烁”相位噪声区域(斜率=–20dB/10倍)还存在x=2、3、4的区域,这些区域依次出现,愈来愈接近载波频率。
图3:振荡器相位噪声(dBc/Hz)与频率偏移的关系
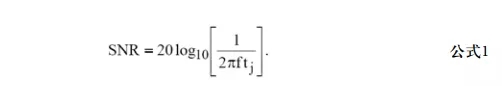
请注意,相位噪声曲线与放大器的输入电压噪声频谱密度有一定的类似。像放大器电压噪声一样,振荡器也非常需要较低的1/f转折频率。
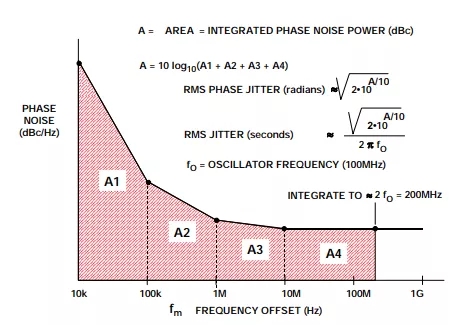
我们已经看到,振荡器通常用相位噪声来描述性能,但为了将相位噪声与ADC的性能关联起来,必须将相位噪声转换为抖动。为将该曲线与现代ADC应用关联起来,选择100MHz 的振荡器频率(采样频率)以便于讨论,典型曲线如图4所示。请注意,相位噪声曲线由多条线段拟合而成,各线段的端点由数据点定
图4:根据相位噪声计算抖动
将相位噪声转换为抖动
计算等效rms抖动的第一步是获得目标频率范围(即曲线区域A)内的积分相位噪声功率。该曲线被分为多个独立区域(A1、A2、A3、A4),各区域由两个数据点定义。一般而言,假设振荡器与ADC输入端之间无滤波,则积分频率范围的上限应为采样频率的2倍,这近似于ADC采样时钟输入的带宽。
积分频率范围下限的选择也需要一定的斟酌。理论上,它应尽可能低,以便获得真实的rms抖动。但实际上,制造商一般不会给出偏移频率小于10Hz时的振荡器特性,不过这在计算中已经能够得出足够精度的结果。多数情况下,如果提供了100Hz时的特性,则选择100Hz作为积分频率下限是合理的。否则,可以使用1kHz或10kHz数据点。
还应考虑,“近载波”相位噪声会影响系统的频谱分辨率,而宽带噪声则会影响整体系统信噪比。最明智的方法或许是按照下文所述对各区域分别积分,并检查各区域的抖动贡献幅度。如果使用晶体振荡器,则低频贡献与宽带贡献相比,可能可以忽略不计。其它类型的振荡器在低频区域可能具有相当大的抖动贡献,必须确定其对整体系统频率分辨率的重要性。
各区域的积分产生个别功率比,然后将各功率比相加,并转换回dBc。一旦知道积分相位噪声功率,便可通过下式计算rms相位抖动(单位为弧度,更多信息及其引申等参见参考文 献3至7):
以上结果除以2πfO,便可将用弧度表示的抖动转换为用秒表示的抖动:应注意,网络上可以找到计算机程序和电子表格来执行分段积分并计算rms抖动,从而大大简化计算过程(参考文献8、9)。
图5给出了一个计算示例,它假设仅存在宽带相位噪声。所选的–150dBc/Hz宽带相位噪声代表了良好信号发生器的特性,由此获得的抖动值可以代表实际情况。–150dBc/Hz的相位噪声(用比值表示)乘以积分带宽(200MHz),得到–67dBc的积分相位噪声。请注意,该乘法相当于把10log10[200MHz–0.01MHz]的量与相位噪声(dBc/Hz)相加。实际上,计算中可以丢弃0.01MHz的频率下限,因为它不会对最终结果产生重大影响。利用公式3可知, 总rms抖动约为1ps。
图5:假设仅存在宽带相位噪声的抖动计算示例
晶体振荡器的相位噪声和抖动一般是最低的,图6给出了几个例子以供比较。所示的全部振荡器都具有20kHz的1/f转折频率,因此相位噪声代表的是白色相位噪声水平。两个Wenzel振荡器为固定频率型,性能出色(参考文献9)。利用可变频率信号发生器很难实现如此高的性能,一个质量相对较高的发生器的性能为–150dBc,如图所示。
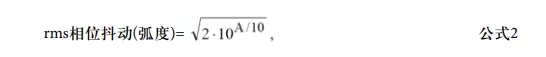
图6:100 MHz振荡器的宽带相位本底噪声比较(Wenzel ULN和Sprinter系列的特性和报价已获得Wenzel Associates的许可)
这里应注意,振荡器的本底噪声存在一个理论限值,它由匹配源的热噪声决定:+25℃时 为–174dBm/Hz。因此,相位噪声为–174dBc/Hz的振荡器以+13-dBm输出驱动50Ω(2.82-Vp-p)负载时,其本底噪声为–174dBc+13dBm=–161dBm。这就是图6所示的Wenzel ULN 系列的情况。
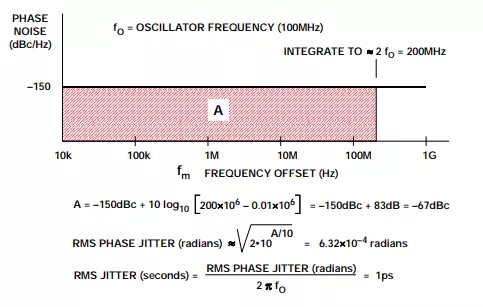
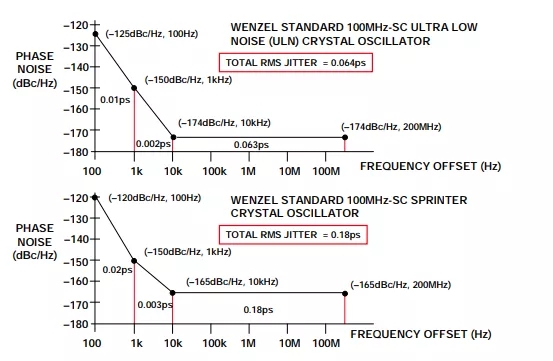
图7给出了两个Wenzel晶体振荡器的抖动计算。每种情况中的数据点直接来自制造商的数 据手册。由于1/f转折频率较低,抖动的绝大部分是由“白色”相位噪声区域引起的。计算值 64fs(ULN-Series)和180fs说明抖动极低。图中分别标出了各区域的噪声贡献,以供参考。总抖动为各抖动贡献因素的方和根
图7:低噪声100MHz晶体振荡器的抖动计算(所用相位噪声数据已获得Wenzel Associates的许可)

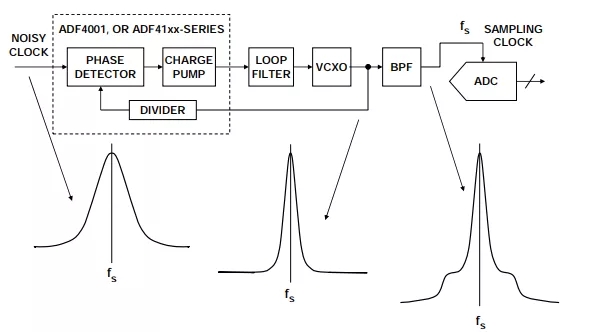
在要求低抖动采样时钟的系统设计中,低噪声专用晶体振荡器的成本一般极高。替代方案是使用锁相环(PLL)和压控振荡器来“净化”高噪声系统时钟,如图8所示。关于PLL设计有许多很好的参考资料(例如参考文献10至13),在此不做进一步探讨,但仅说明一点:使用 窄带宽环路滤波器和压控晶体振荡器(VCXO)通常可获得最低的相位噪声。如图8所示, PLL在降低整体相位本底噪声的同时,往往也会降低“近载波”相位噪声。在PLL输出之后连接一个适当的带通滤波器,可以进一步降低白色本底噪声
图8:使用锁相环(PLL)和带通滤波器来调理高噪声时钟源
在PLL中内置一个自由运行VCO的效果如图9所示。注意,由于PLL的作用,“近载波”相位噪声大幅降低。
图9:自由运行的VCO和连接PLL的VCO的相位噪声
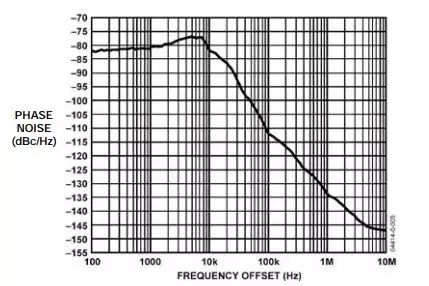
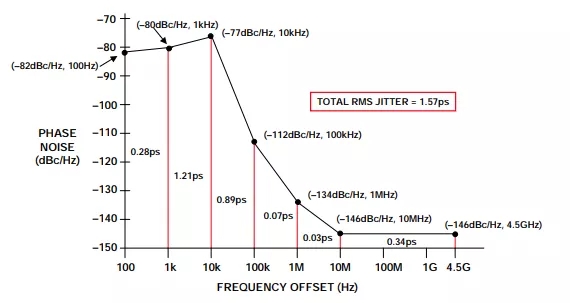
ADI提供许多不同的频率合成产品,包括DDS系统、整数N和小数N分频PLL等。例如,ADF4360系列是内置VCO的完全集成式PLL。在结合使用一个10kHz带宽环路滤波器的情况下,ADF4360-1 2.25-GHz PLL的相位噪声如图10所示,分段近似和抖动计算如图11所示。请注意,即使采用非晶体VCO,rms抖动也只有1.57ps。
图10:采用10 kHz带宽环路滤波器的ADF4360-1 2.25-GHz PLL的相位噪声
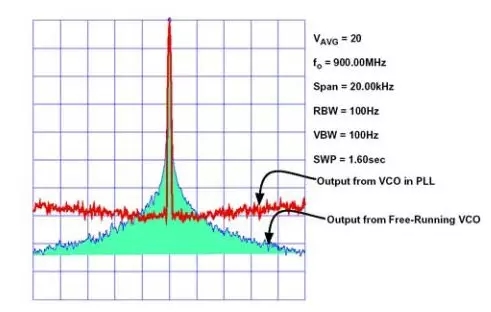
图11:ADF4360-1 2.25-GHz PLL相位噪声的分段近似抖动计算
一直以来,PLL设计高度依赖于教科书和应用笔记来帮助设计环路滤波器等。现在,利用ADI提供的可免费下载的ADIsimPLL?软件,PLL设计变得非常轻松。要开始设计,请输入所需的输出频率范围以选择一个电路,然后选择PLL、VCO和晶体参考。一旦选定环路滤波器配置后,就可以分析电路并从频域和时域两方面优化相位噪声、相位裕量、增益、杂散水平、锁定时间等。程序还能根据PLL相位噪声计算rms抖动,以便评估作为采样时钟的最终PLL输出。
结束语
采样时钟抖动可能会给高性能ADC的信噪比性能带来灾难性影响。虽然信噪比与抖动之间的关系已为大家所熟知,但大多数振荡器都是用相位噪声来描述特性的。本文说明了如何将相位噪声转换为抖动,以便轻松计算信噪比的下降幅度。
ADF4360-1
输出频率范围:2050 MHz至2450 MHz
2分频输出
3.0 V至3.6 V电源供电
1.8 V逻辑兼容
整数N分频频率合成器
可编程双模预分频器:8/9、16/17、32/33
可编程输出功率水平
三线式串行接口
模拟和数字锁定检测
使用晶体VCO(以及适当的滤波)的现代PLL虽然不如成本高昂的独立晶体振荡器那样理想,但也能实现出色的抖动性能,适合除要求最为苛刻的应用之外的大部分应用。 由于低抖动要求,整个时钟分配问题变得更加重要。